Introduction
Natural fish roes such as salmon roe, caviar, and flying fish roe and so on are decreasing in the production owing to marine pollution, overfishing, destruction of spawning grounds, and climate changes (Jackson et al., 2006). The supply of natural fish roe cannot meet the demand, so the demand to fish roe analogs is increasing on the market. Fish roe analogs are regarded as a high value added processing technology that enables a stable supply of goods, hygienic quality control, and development of various favorite foods. Encapsulation technology is applying for the production of fish roe analogs. Encapsulation refers to the technology processing as bead or capsule types by entrapping active compounds in polymer matrices, which are form of particulate (Lee et al., 2013). The size of the capsule can range from micrometers to millimeters and even if the ideal shape is spherical, the shape is greatly affected by the structure of the original material prior to encapsulation (Cho et al., 1997). The encapsulation technology is widely used for immobilizing, stabilizing and controlling release of active compounds (Chan et al., 2009). Alginic acid has been widely used as polymer materials for encapsulation. Alginic acid, which is a polysaccharide obtained from a brown algae, is a linear block copolymer in which β-D-mannuronate (M) and α-L-guluronate (G) are linked through a β-1,4 or a α-1,4 glycosidic bond (Pielesz et al., 2008; Gryshkov et al., 2014). It is capable of forming gel in a relatively mild condition in the presence of cations (Vandenberg et al., 2001). The gel is formed by an ionic interaction between a multivalent cations and G residues from alginate chain, and the mechanism can be explained by the ‘egg-box’ model (Hoad et al., 2011). The gel formation proceeds by cross-linkages of a threedimensional structure between alginate and calcium ions when calcium ions are added to an alginate aqueous solution (Clark & Ross-Murphy, 1987; Rousseau et al., 2004). The properties of alginate gels are strongly dependent on the ratio of uronic monomers, sequence, cation concentration in the reaction solution, and curing time (SmidsrØd, 1974; Draget et al., 1994; Velings & Mestdagh, 1995; Ouwerx et al., 1998). In the food industry, alginate beads or capsules can be formed through the gelation reaction. Alginates are also used as a material for encapsulation in a variety of fields including bioprocess, pharmacology, and food and feed industries (Vandenberg et al., 2001; Pielesz et al., 2008; Chan et al., 2011; Gryshkov et al., 2014). Alginate gel is also used not only in immobilized cells, enzymes, and drug carriers of protein but also in the drug release control system due to the properties such as being an ingredient of natural origin, biocompatibility, and relatively low cost of production (Pielesz et al., 2008). The production of fish roe analogs using alginate gel was often influenced on their physical properties such as size, sphericity, rupture strength etc. according to processing conditions. Ji et al. and Woo et al. reported on the sphericity optimization of beads using alginate gels and on the production of caviar analogs using calcium alginate gels with single nozzle. The present study aims to optimize physicochemical conditions for sphericity of the capsule type-fish roe analogs using equipment with double nozzles. For the setting of optimal sphericity conditions, sodium alginate concentration (%, w/v), calcium chloride concentration (%, w/v), agitation speed of a reactor (rpm), and dropping height (cm) were investigated by response surface methodology with central composite design.
Materials and Methods
Sodium alginate and calcium chloride as main materials for fish roe analogs manufacture were purchased from Junsei Chemical Corporation (Tokyo, Japan). All other chemicals and reagents used in this study were analytical grade.
Sodium alginate solution and soybean oil were dropped into calcium chloride solution through the corresponding nozzles (Fig. 1). The optimal conditions for manufacturing of the analogs were set up by manipulating sodium alginate concentration (%, w/v), concentration of calcium chloride (%, w/v), agitation speed of calcium chloride solution in the reactor (rpm), and dropping height between the tip of the nozzle and the surface of the reactor (cm). The sodium alginate solution was prepared at the ranges of 1.2, 1.5, 1.8, 2.1, and 2.4% (w/w). The sodium alginate solution was flowed into calcium chloride solution of a different concentration (0.5, 1.0, 1.5, 2.0, and 2.5%, w/w) through the outer nozzle (1 mm in inner diameter × 3 cm in length) of double nozzles at the speed of 1.5 mL/sec using peristaltic pump (Micro tube pump MP-3N, Eyela, Tokyo, Japan). Soybean oil was also flowed into calcium chloride solution of a different concentration through the inner nozzle (0.28 mm in inner diameter × 4.4 cm in length) of the double nozzles at the speed of 0.58 mL/s using another peristaltic pump (Cassette tube pump SMP-23, Eyela, Tokyo, Japan). The calcium chloride solution was agitated at a different speed (150, 220, 290, 360, and 430 rpm) by a magnetic stirrer. The volume of calcium chloride solution in reactor was based on 250 mL and the reaction time was 3 min at an ambient temperature. The dropping height between the tip of the double nozzles and the surface of the calcium chloride solution was ranged from 5, 10, 15, 20, and 25 cm. After the reaction during 3 min in calcium chloride solution, the resultant analogs were separated from the calcium chloride solution using a sieve and then washed with distilled water. The analogs were kept at an ambient temperature until measuring their sizes and sphericity.
The size of the analogs was measured by an optical microscope (15× magnifications, BX-50, Olympus, Tokyo, Japan) with Motic Images Plus 2.0 program. The measurement was conducted by choosing five random the analogs and then the average of their maximum diameters and minimum diameters was determined as size of the analogs. The sphericity was indicated as the percentage ratio of the minimum diameter to the maximum diameter of five random the analogs.
Manufacturing process of the analogs was estimated by using a central composite design and the optimization for sphericity of the analogs was conducted by response surface methodology. A central composite design was composed of the factorial portions of 24, the axial portions of 8, and the central point of triplicate repeats in experimental design (Table 2). In order to determine optimal sphericity conditions for manufacturing of the analogs, sodium alginate concentration (X1, %), concentration of calcium chloride solution (X2, %), agitation speed of calcium chloride solution in the reactor (X3, rpm), and dropping height between the tip of the double nozzles and the surface of the calcium chloride solution (X4, %) were used as independent variables. The portion values and ranges about 4 independent variables were based on the preliminary experiment (Table 1). It was randomized for experimental runs to minimize the effects of unsuspected variability in the surveyed responses. The response surface regression procedure for statistical analysis of the analogs was carried out using SAS software (Version 14, Minitab Inc., State College, PA, USA). It was used to fit the following quadratic polynomial equation.
In this polynomial equation of quadratic, Y is the dependent variable, Xi and Xj are the normalized independent variables, β0 is constant, and βi, βii, βij are regression coefficients. Response optimization for physicochemical parameters was heuristically calculated by the desirability function of MINITAB statistical software (Version 14, Minitab Inc., State College, PA, USA), to find the conditions satisfying a dependent variable, sphericity (Y, %) of the analogs. The response surface plots were presented with a three-dimensional graph using Maple software (Maple 7. Waterloo Maple Inc., Canada) and represented correlation between two independent variables and the dependent variable which is sphericity (Y, %) of the analogs.
Results and Discussion
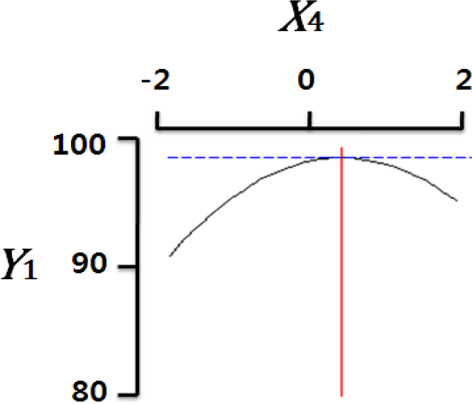
The response surface regression of SAS software was used to fit the quadratic polynomial equation about the results of the experiment for optimization of sphericity of the analogs. All the coefficients of linear (X1, X2, X3, X4), quadratic (X1X1, X2X2, X3X3, X4X4), and interaction (X1X2, X1X3, X1X4, X2X3, X2X4,X3X4) were estimated for significance based on t-statistic and the results for sphericity of the analogs were presented in Table 3. All the linear coefficients except for the X4 (dropping height, cm) had a high significant difference (p<0.01). As the X4 term was 0.1680, it was not significant (p>0.05). All of the quadratic coefficients were significant as p<0.05. On the other hand, all the interaction was not significant. The fitted response surface model for manufacturing condition of the analogs is a follow equation:
The model was explained as the equation which is eliminated all the insignificant coefficients (p>0.05) for fitness. The coefficient of determination was 0.9080, which means how suitable the selected parameters express the correlation. When the value of R2 is generally over 0.9, the response surface model has significant correlation for sphericity of the analogs. Thus, the quadratic polynomial model was significant within the limit of p<0.01.
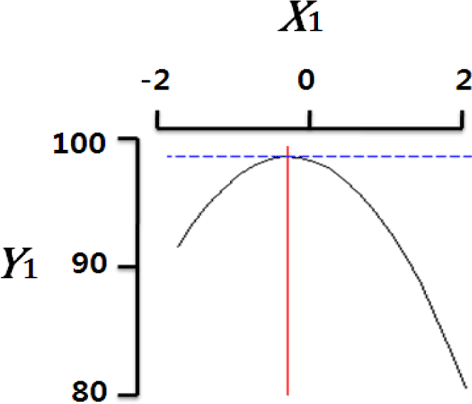
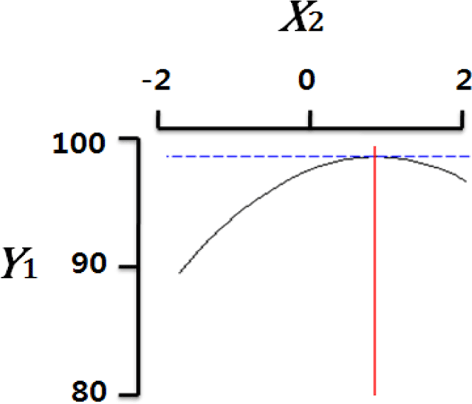
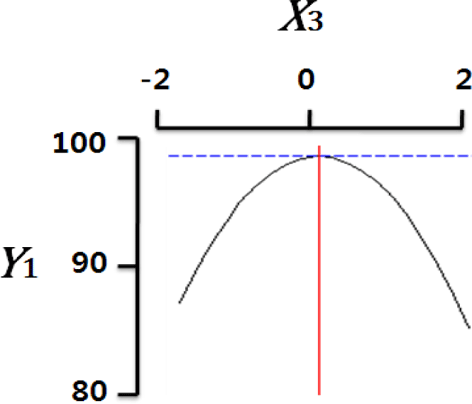
Fig. 2 shows the three-dimensional graph created by using Maple software with the results of response surface analysis to examine the effect of four important factors (X1, sodium alginate concentration; X2, calcium chloride concentration; X3, agitation speed of calcium chloride solution; X4, dropping height) selected as independent variables on the sphericity (Y) of the analogs. As four independent variables have a considerable effect on shape and size of the analogs, they are also closely related with sphericity (Y). To find which variables have a great effect on sphericity among four independent factors, the interrelations between two random independent variables and a dependent variable were indicated as the response surface plots of six. As a result, effects of the independent variables on the sphericity of the analogs varied each other. The sphericity markedly decreased in the case of sodium alginate (0 to 2.0; Fig. 2 A and E), because concentrations of two solutions affected gelation rate and capsule shape. Alginate solution which possesses a low viscosity cannot able to keep their sphericity against the drag forces upon clash with the surface of the calcium chloride solution in the reactor, on the other hand, alginate solution which has a high viscosity is not suitable to encapsulation between two solutions (Seifert & Philips, 1997). The increase of calcium chloride concentration also makes more spherical capsule according to the increase of gelation kinetics (Chen et al., 2006). Therefore, the concentration of X1 and X2 acted as critical factors on spherical shape of the analogs.
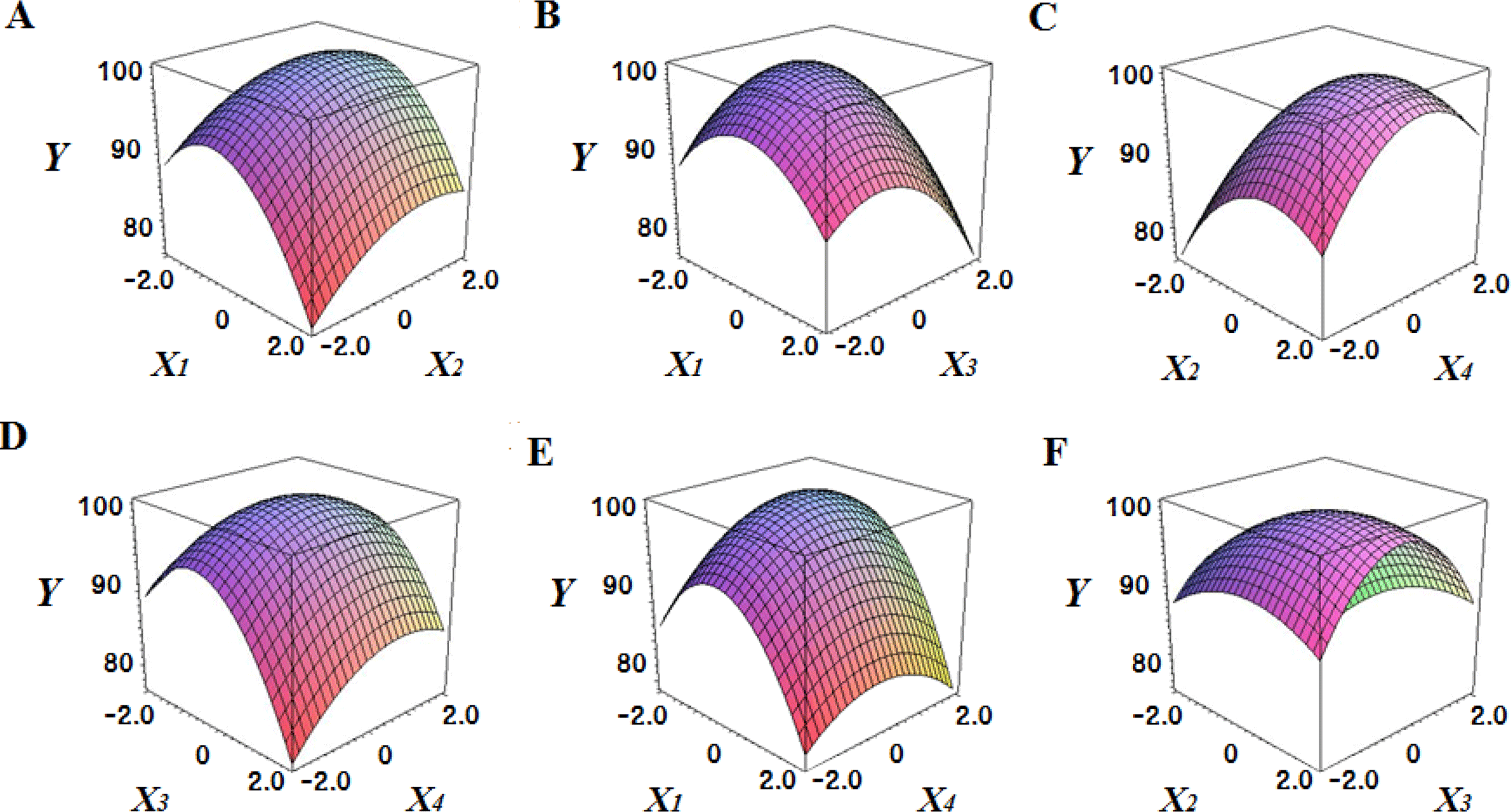
Table 4 shows the optimum conditions of independent variables for manufacturing process of the analogs. Four independent variables (X1, X2, X3, X4) were designated as important independent variables of central composite design through the preliminary experiment for manufacturing of the analogs. Central values of independent variables established in the preliminary experiment were coded as zero, respectively. In order to optimize dependent variable (sphericity, Y) statistically, response optimizer function of SAS software was used. Predicted conditions of independent variables were reasoned as coded and uncoded values. As the actual values (uncoded values) of independent variables were X1=1.66%, X2=1.86%, X3=280 rpm, and X4=17 cm, the predicted value of the response was 99.7%. In the four graphs relating to coded values (Table 4), the values of all the independent variables were calculated more high/low as compared with the experimental optimal conditions, 0. The X2 term (calcium chloride) was especially differential, which means concentration of calcium chloride solution was critical position in optimizing sphericity. Generally, a gelation occurs when alginate-droplet falls into a calcium chloride solution. The ionic interaction between G-blocks from two or more alginate chains and calcium cations formulates a three dimensional network of alginate molecules, and the formation of hydrogel network during cross-link is explained as ‘Egg-box’ model (Lee et al., 2013). High concentration of calcium chloride leads capsules with more homogeneous network. As the increase of Ca2+ ions concentration, the gelation kinetics is also accelerated, which makes more rapid stabilization and entrapment of capsule analogs (Chen et al., 2006). So, capsules with more spherical shape and uniform size are manufactured with increase of the concentration of calcium chloride (Chen et al., 2006; Smrdel et al., 2008). To verify the accuracy of the predicted Y values, the capsule type-fish roe analogs were prepared under the optimal conditions. As compared to the predicted value, the experimental value was 99.8±0.77 through the triplicate repeats. Although the experimental value showed a slightly higher than the predicted value, both are about the same. Accordingly, the estimated response surface model was suitable for optimization of manufacturing process of the analogs.
Conclusion
The present study set four major factors such as sodium alginate concentration, calcium chloride concentration, agitation speed, and dropping height that affect to production of the capsule type-fish roe analogs as independent variables. The optimum conditions for the analogs processing were investigated using response surface methodology with central composite design. The optimum conditions were 1.66% sodium alginate, 1.86% calcium chloride, agitation speed of calcium chloride solution at 280 rpm, and dropping height at 17 cm between the tip of nozzle and the surface of calcium chloride solution in reactor. As a result, the predicted value for the sphericity of the response was 99.4±0.21% and the experimental value was 99.8±0.77%. Sphericity is a very important factor for processing of the analogs. The manufactured analogs showed a high sphericity near a complete spherical shape. Alginate gels have been mostly processed as bead types using single nozzle. The present study elucidated manufacturing conditions of the capsule type-fish roe analogs with a high sphericity near the natural ones using double nozzles. The results are considered to play an important role for a potential application to substitutes of natural ones as well as development of other analog foods.